Algebra 2 Unit 10 Polynomial and Rational Functions Unit Review
A set of algebra 2 problems with their detailed solutions to self examination and diagnose your background and review and gain deep agreement on the following topics:
Complex Numbers
Problem ane-1
Let z = two - 3 i where i is the imaginary unit. Evaluate z z* , where z* is the conjugate of z , and write the respond in standard form.
Detailed Solution.
Trouble ane-two
Evaluate and write in standard grade \( \dfrac{1-i}{2-i} \) , where i is the imaginary unit.
Detailed Solution.
Quadratic Equations
Trouble 2-i
Find all solutions of the equation \( 10(x + 3) = - v \).
Detailed Solution.
Problem 2-2
Find all values of the parameter m for which the equation \( -2 x^two + thousand x = 2 g \) has complex solutions.
Detailed Solution.
Functions
Problem 3-ane
Allow \( f(10) = - x^2 + three(x - 1) \). Evaluate and simplify \( f(a-one)\).
Detailed Solution.
Problem 3-2
Write, in interval note, the domain of function \(f\) given by \(f(ten) = \sqrt{ten^2-16} \).
Detailed Solution.
Trouble 3-3
Notice and write, in interval notation, the range of function \(f\) given by \(f(10) = - x^2 - 2x + 6 \).
Detailed Solution.
Problem 3-4
Allow \(f(x) = \sqrt{ten - 2} \) and \(g(x) = x^2 + 2 \); evaluate \( (f_o one thousand)(a - 1) \) for \( a \lt 1 \).
Detailed Solution.
Problem 3-5
Which of the post-obit is a one-to-ane part?(There may be more one answer).
a) \(f(10) = - 2 \) b) \(one thousand(x) = \ln(x^2 - i) \) c) \(h(x) = |x| + ii \) d) \(j(ten) = one/x + 2 \) e) \(thousand(x) = \sin(x) + two \) f) \(l(x) = ln(x - ane) + 1 \)
Detailed Solution.
Problem iii-half dozen
What is the changed of role f given by \(f(x) = \dfrac{-x+two}{x-ane}\)?
Detailed Solution.
Trouble 3-7
Classify the post-obit functions equally even, odd or neither.
a) \(f(10) = - x^3 \) b) \(g(ten) = |x|+ 2 \) c) h(x) = \( \ln(x - 1) \)
Detailed Solution.
Problem 3-8
Function \(f \) has ane zero but at \(ten = -ii\). What is the naught of the function \(2f(2x - v) \)?
Detailed Solution.
Trouble 3-9
Which of the following piecewise functions has the graph shown below?
a) \( f(x) = \brainstorm{cases} x^ii & \text{if} \; x \ge 0 \\ 2 & \text{if} \; -two \lt x \lt 0\\ - ten + ane& \text{if} \; x \le -two \cease{cases} \) b) \( thousand(x) = \begin{cases} ten^2 & \text{if} \; ten \gt 0 \\ 2 & \text{if} \; -2 \lt x \le 0\\ - ten + 1& \text{if} \; x \le -2 \end{cases} \) c) \( h(x) = \begin{cases} x^ii & \text{if} \; 10 \gt 0 \\ ii & \text{if} \; -2 \lt x \lt 0\\ - x + ane & \text{if} \; x \lt -2 \end{cases} \)
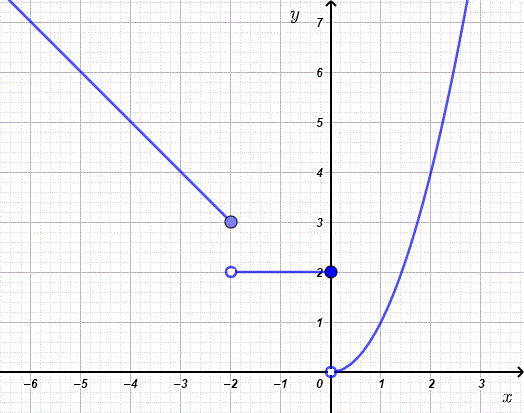


Detailed Solution.
Problem 3-x
Calculate the boilerplate rate of change of function \( f(10) = \dfrac{1}{x} \) as x changes from \( 10 = a\) to \( 10 = a + h \).
Detailed Solution.
Polynomials
Problem 4-1
Observe the caliber and the residuum of the division \( \dfrac{-ten^four+2x^3-10^2+five}{10^2-ii} \).
Detailed Solution.
Problem 4-2
Find \( thousand \) so that the remainder of the division \( \dfrac{iv x^2+2x-3}{two x + one thousand} \) is equal to \( -1 \)?
Detailed Solution.
Problem iv-3
\( (x - 2) \) is 1 of the factors of \( p(10) = -2x^4-8x^iii+2x^ii+32x+24 \). Factor \(p\) completely.
Detailed Solution.
Problem four-4
Factor \( 16 ten^four - 81 \) completely.
Detailed Solution.
Problem 4-five
Find all solutions to the equation \( (x - 3)(x^ii - four) = (- 10 + 3)(x^two + 2x) \)
Detailed Solution.
Problem four-6
Solve the inequality \( (x + two)(x^2-4x-5) \ge (-x - 2)(10+1)(x-3)\)
Detailed Solution.
Trouble iv-7
The graph of a polynomial function is shown beneath. Which of the following functions can possibly take this graph?
a) \( y = -(x+ii)^5(x-1)^2 \) b) \( y = 0.5(x+ii)^3(x-1)^2 \) c) \( y = -0.v(10+two)^three (x-1)^two \) d) \( y = -(x+ii)^3(x-1)^ii \)



Detailed Solution.
Problem four-viii
Which of the following graphs could peradventure exist that of the part f given by \( f(ten) = k (x - 1)(x^ii + 4) \) where k is a negative constant? Find thousand if possible.
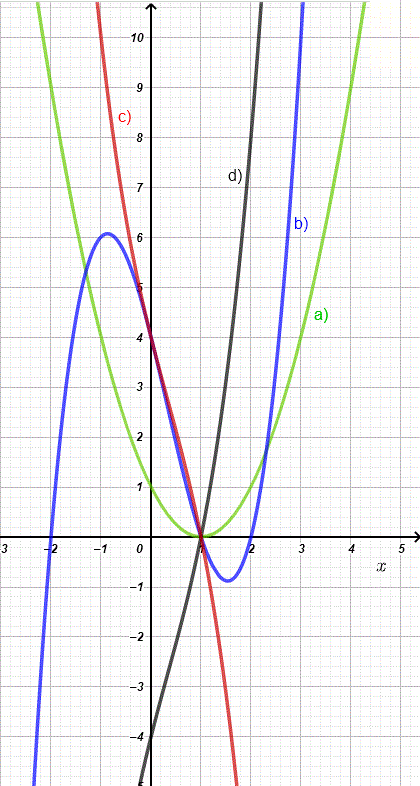


Detailed Solution.
Rational Expressions, Equations, Inequalities and Functions
Problem 5-ane
Write equally a single rational expression: \( \dfrac{x^2+3x-5}{(x-1)(x+2)} - \dfrac{2}{x+2} - 1 \).
Detailed Solution.
Problem 5-ii
Solve the equation: \( \dfrac{- x^two+5}{x-1} = \dfrac{ten-2}{10+2} - 4 \).
Detailed Solution.
Problem 5-iii
Solve the inequality: \( \dfrac{1}{x-i}+\dfrac{1}{10+1} \ge \dfrac{3}{10^2-1} \).
Detailed Solution.
Problem v-iv
Find the horizontal and vertical asymptotes of the function: \( y = \dfrac{3x^2}{v x^ii - 2 10 - 7} + ii \).
Detailed Solution.
Problem five-5
Which of the following rational functions has an oblique asymptote? Find the indicate of intersection of the oblique asymptote with the function.
a) \( y = -\dfrac{x-1}{x^2+2} \) b) \( y = -\dfrac{x^4-ane}{x^2+two} \) c) \( y = -\dfrac{10^three + 2x ^ two -1}{x^ii- 2} \) d) \( y = -\dfrac{x^2-ane}{x^2+two} \)
Detailed Solution.
Problem v-6
Which of the post-obit graphs could be that of office \( f(x) = \dfrac{2x-two}{x-1} \)?
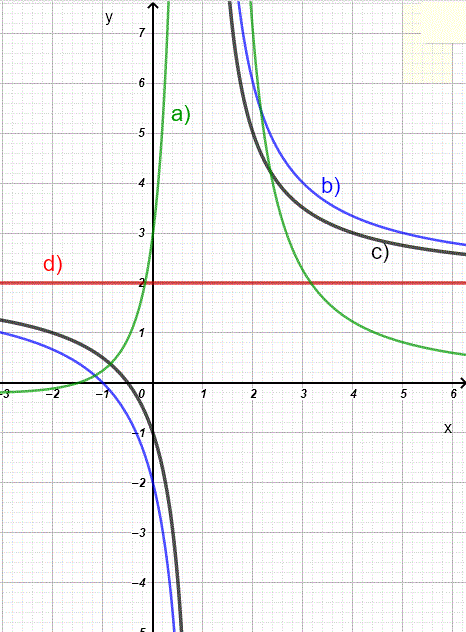


Detailed Solution.
Trigonometry and Trigonometric Functions
Trouble 6-1
A rotating bike completes yard rotations per minute. Determine the athwart speed of the wheel in radians per second.
Detailed Solution.
Trouble six-two
Determine the verbal value of \( sec(-11\pi/3) \).
Detailed Solution.
Trouble 6-iii
Convert 1200� in radians giving the exact value.
Detailed Solution.
Problem half-dozen-four
Convert \( \dfrac{-7\pi}{9} \) in degrees giving the exact value.
Detailed Solution.
Problem 6-v
What is the range and the menstruum of the the function \( f(10) = -two\sin(-0.5(x - \pi/5)) - six \)?
Detailed Solution.
Problem half-dozen-half dozen
Which of the following graphs could be that of function given by: \( y = - \cos(2x - \pi/4) + 2 \)?



Detailed Solution.
Problem half dozen-7
Find a possible equation of the course \( y = a \sin(b x + c) + d \) for the graph shown beneath.(in that location are many possible solutions)



Detailed Solution.
Problem half-dozen-8
Find the smallest positive value of x, in radians, such that \( - four \cos (2x - \pi/iv) + 1 = iii \)
Detailed Solution.
Trouble six-9
Simplify the expression: \( \dfrac{\cot(x)\sin(x) + \cos(x) \sin^2(10)+\cos^3(x)}{\cos(x)} \)
Detailed Solution.
Logarithmic and Exponential Functions
Problem 7-ane
Simplify the expression \( \dfrac{4x^two y^viii}{8 ten^3 y^5} \) using positive exponents in the final answer.
Detailed Solution.
Problem 7-2
Evaluate the expression \( \dfrac{3^{i/iii} ix^{ane/3}}{4^{one/2}} \).
Detailed Solution.
Problem 7-3
Rewrite the expression \( \log_b(2x - 4) = c \) in exponential form.
Detailed Solution.
Problem vii-4
Simplify the expressiomn: \( \log_a(9) \cdot \log_3(a^2) \)
Detailed Solution.
Problem 7-five
Solve the equation \( \log(x + 1) - log(ten - 1) = ii \log(x + ane) \).
Detailed Solution.
Trouble seven-six
Solve the equation \( e^{2x} + e^x = 6 \).
Detailed Solution.
Problem 7-7
What is the horizontal asymptote of the graph of \( f(10) = 2 ( - 2 - e^{x-ane}) \)?
Detailed Solution.
Problem 7-eight
What is the vertical asymptote of the graph of \( f(10) = log(2x - six) + iii \)?
Detailed Solution.
Problem 7-9
Lucifer the given functions with the graph shown beneath?
A) \( y = 2 - 0.v^{2x-1} \) B) \( y = 0.5^{2x-1} \) C) \( y = two - 0.five^{-2x+ane} \) D) \( y = 0.5^{-2x+1} \)
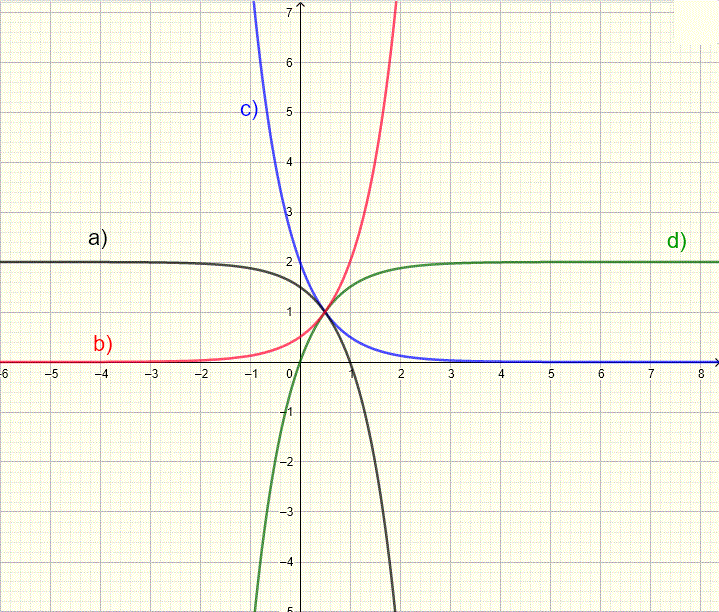


Detailed Solution.
Problem 7-10
Lucifer the given functions with the graph shown below?
A) \( y = 2+ln(x-two) \) B) \( y=-log_2(x+one)-1 \) C) \( y = -ln(-x) \) D) \( y = y=-log_3(x+1)-i \)
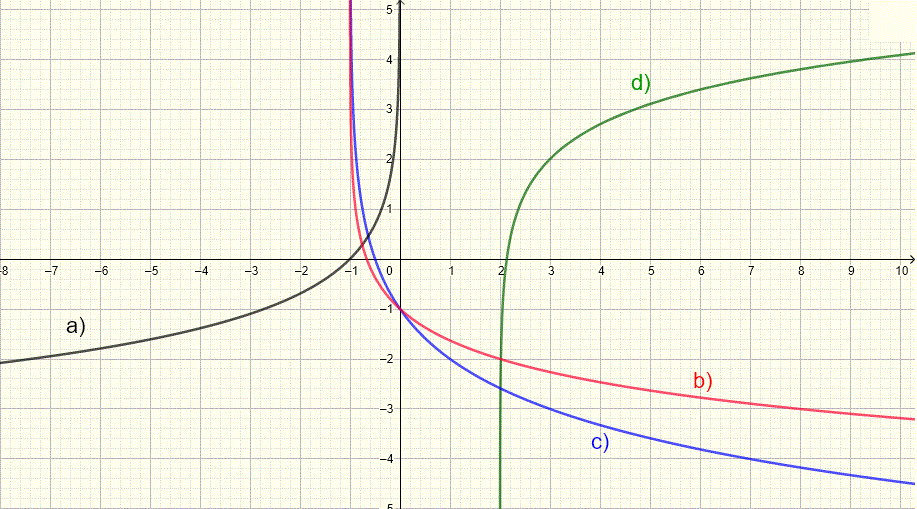


Detailed Solution.
armstrongblith1981.blogspot.com
Source: https://www.analyzemath.com/Algebra2/Algebra-2.html
0 Response to "Algebra 2 Unit 10 Polynomial and Rational Functions Unit Review"
Post a Comment